Spelunking
Did I mean the game Spelunky?? Unfortunately, I didn’t, but
here’s a picture of what the game looks like in case you wanted to see.
It’s too bad this isn’t what I’m analyzing because it looks
pretty fun and apparently it won PC game of the year in 2013.
Moving on to what I’ll actually be talking about…
Searching
for the lost spelunker:
-Some things you need to know-
-spelunkers
are people who explore systems of caves wither on land or underwater
-We are
trying to find an unfortunate spelunker who has become lost in the cave :O
-While attempting to find this spelunker
he may be wandering around and not just staying in one place
This is very similar to the cop vs invisible robber that Madison
talked about, it’s just that in this case what is the “robber” is not trying to
evade, but instead trying to be found. Although this can be used to find an
invader as well, which would make it exactly the same as the cop vs invisible
robber.
Different
Graphs and Their Number of Searchers:
As I was going through the different types of graphs given and
the number of searchers correlated with these given graphs I had a realization;
all the graphs here have the same number of searchers needed as the number of
cops needed in regular cops and robbers!
-Path Graphs-

Can be searched with one searcher
-Cycle Graphs-
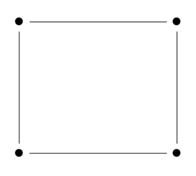
Can be searched with two searchers
-Star Graphs-
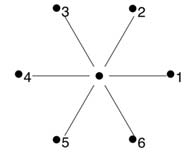
Can be searched with 2 searchers.
-Complete Graphs-
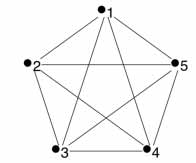
Can be searched with n searchers where n is the number of
vertices.
In these next two methods of searching, the searchers are to
search for the spelunker down each corridor, or edge, within the graph. This is
assuming that the cave is known and the people have to go down the whole
corridor in order to see the spelunker instead of just looking down the
corridor and being able to see him. Each searcher is able to move at the same
time.
One-tick
Searching:
Each searcher is only allowed to move one time. This means
that you would need the same number of searchers as there are edges in a graph.
This is obviously the fastest way to search a graph since each person moves at
once and you will find the spelunker who’s lost on the first move.
Although this is nice and fast it’s not really all that feasible.
In the example given in the website I was looking at there was a square graph
indicating there were four corridors within the cave and I mean really, how many
caves have only four corridors in them? You’d need a whole lot of people all at
once and there just aren’t going to be that many.
This brings us to…
Two-tick
Searching:
This time, as the name suggests, each searcher is allowed to
move at most twice. An example is shown below.
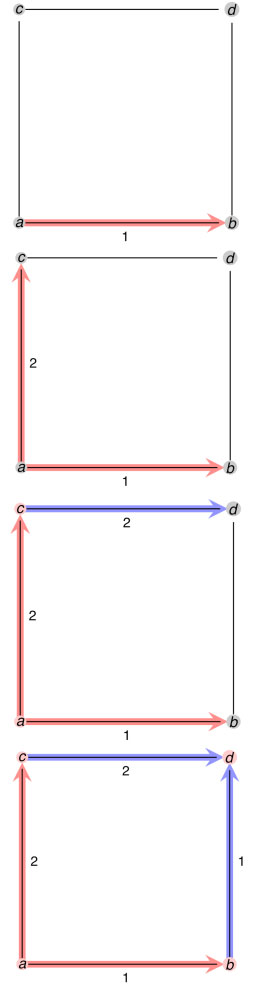
In this example there are only two people needed as opposed
to the four that would be needed if we were doing the one-tick searching. This
gives the number of moves the spelunker can be found in to be at least two.
Conclusion:
Searching for a lost spelunker is very similar to cop vs the invisible robber and has the same amount of cops, in this case searchers, needed for simple graphs as regular cops and robbers do. These two ways of searching lead to a fast discovery of the spelunker, but aren't all that realistic.
http://mathcentral.uregina.ca/beyond/articles/PIMS/IPSW2009/spelunking/solution.html
Assuming that the spelunker is trying to be found, is he going to move around the graph? Or do we assume that he stays put all the time and that the searchers are the ones moving until they find him? Does his movement affect the time he's found in?
ReplyDeleteI too wondered this! Also, for a complete graph with n vertices, since you are able to use n searchers, are we able to place a searcher on every vertex? Thus locating the spelunker in one move?
DeleteHe can be moving around the graph, but in these two cases that doesn't matter since all of the edges will be searched within the first or second move. In other cases it would affect the time he's found in since every edge wouldn't be searched within the first two moves.
DeleteIn your star graph example why would we need two searchers? Wouldn't we only need one whether the people move simultaneously or not? The searcher could start on say the middle vertex and the spelunker on one of the outer edges and the searcher would have to go back to the middle vertex to get to the other "caves" (vertices) and if we assume that the spelunker is moving, then there is a good chance that he will be found since he too must go to the middle vertex?
ReplyDeleteThat makes sense if we assume the spelunker is moving but I don't think we can assume that.
DeleteSo if my thinking is correct, there are two ways in which one searcher could fail to find the spelunker,
1. Both the spelunker and the searcher stay put waiting for each other
2. Both players are moving simultaneously and whenever the searcher moves from the middle vertex, the spelunker moves towards it and they take turns searching in separate branches of the graph.
I like your thinking on that star graph Mac. Hopefully that situation would never happen in real life with one searcher :/ However, I'm wondering if there are any rules in which the searcher never stops moving and the lost spelunker always stays put? This may be applicable to a real life survival scenario.
DeleteHmm... well, if I were wandering around in a cave and realized I was lost, I might try staying put for a little while. Can you say anything about what a good strategy for a cop would be in that situation? (Hint: try looking up "cop vs. sitter" or "cop vs. immobile hider" for some pretty thorough explanations of how that would work.)
ReplyDeleteAre there any other strategies for the spelunker that might be helpful to the search party? And what else might a search party be able to do besides the one-tick and two-tick methods you describe above?