Cop, Robber, and Alarms is a game played with one cop and partial information about the location of the robber. In this game, the cop receives partial information from "alarms", which are placed on some of the vertices of the graph. When the robber lands on a vertex with an alarm, the cop learns of the robber’s position. However, the cop does not know which direction the robber goes after leaving an alarmed vertex. We will try to find and characterize the minimum number of alarms required, denoted A(G), to guarantee the capture of the robber on a copwin graph G.
First, we will look at one scheme for placing alarms on vertices of a specific kind of tree: a k-ary tree.
What is a k-ary tree? Read on!
Definitions
The neighborhood of a vertex v in a graph G, denoted N(v), is the set of vertices adjacent to v.
Example (below): the neighborhood of vertex a, N(a) = {r, b, e}.
A rooted tree is a tree with one vertex r chosen as root.
The graph below is a rooted tree with vertex r chosen as the root.
For each vertex v, let P(v) be the unique v, r-path.
Example: P(c) = c, b, a, r
The parent of v is its neighbor on P(v).
Example: the parent of c is b.
The children of v are its other neighbors.
Example: c does not have any children because it is a leaf, but the children of b are c and d.
A full complete k-ary tree is a tree where all vertices except the leaves have exactly k children, and the distance between the root and all leaves is the same.
The graph below is a full complete k-ary tree where k = 2. The distance between the root and each leaf is 3. All vertices except the leaves have two children.
The depth of a full tree is defined to be the distance between the root and all leaves.
Example: The depth of the tree below is 3.
Alarms on k-ary Trees
· All leaves remain unalarmed
· All vertices at distance d ≡ 0 (mod 5) from the leaves receive alarms
· The vertices in between (vertices at distance d ≡ i (mod 5), i ≠ 1 from the leaves) have exactly one unalarmed child.
By following the scheme laid out above, we can come up with this arrangement of alarms where the alarms are shown as red dots. By following the guidelines above, other alarm arrangements exist but with the same number of alarms. Comment with another arrangement of alarms!
From this, we get the following theorem…
Theorem: Let T be a full complete k-ary tree of depth m. Then...
We can check this theorem for our k-ary tree above by plugging in k = 2, and m = 3.
Several other schemes for copwin graphs have been developed which are different from the scheme for k-ary trees given above.
Alarms on Copwin Graphs
We need some more definitions first…
Copwin Ordering and Copwin Spanning Tree
A finite graph is copwin if and only if it has a copwin ordering. This means that a graph is copwin if and only if it can be reduced to a single vertex, vn, by successively removing corners.
A graph G is dismantlable if there is an ordering (v1, v2, . . . , vn) of the vertices of G such that for each i < n, vi is a corner in the subgraph induced by {vi , vi+1, . . . , vn}. Such an ordering of the vertices is called a copwin ordering.
This is confusing in words but makes more sense with a picture...
Jeliazkova, Diana. 2006. Aspects of the cops and robber game played with incomplete information. Acadia University.
The copwin graph above has a copwin ordering (11, 12, 13, 10, 6, 7, 8, 9, 5, 2, 3, 4, 1). This means we begin eliminating corners with any of the vertices 11, 12, 13, or 10. We now consider the graph without those vertices to the right. We can see that 6, 7, 8, and 9 are all corners so we can remove them as well. We move to the right in the diagram where all vertices except 1 are corners. Hence, we are left with a single vertex.
A spanning tree constructed from a copwin ordering of G keeps track of the removal of corners. A copwin Spanning Tree, S, is constructed as follows:
Let Gi be the induced subgraph of G, such that Gi = Gi−1 − vi−1, for all i = 2, 3, . . . , n, and G1 = G. In more simple terms, Gi is the graph G after the successive removal of corners {v1, v2, . . . , vi−1}.
For example, from the graph above, G1 is the original graph. G2 = G1 – 11 and G3 = G2 – 12 and so forth where the numbers being subtracted are single vertices.
Let fi : Gi → Gi+1 be the retraction map from Gi to Gi+1, which maps the corner vi onto a vertex that dominates vi in Gi .
Consider a fixed copwin ordering (v1, v2, . . . , vn) of G. The start vertex of the copwin ordering, vn, will be the root of the spanning tree, and for all vertices v1, v2 ∈ V (G), v1v2 ∈ E(S) if and only if fj (v1) = v2 or fj (v2) = v1, for some j.
In our example from the copwin graph above, vn = 1 so 1 will be the root of the spanning tree. Let’s consider the example i = 2. We can see that v2 = 12 from our copwin ordering. So we know that moving from G2 to G3, we took away the vertex labeled 12. So this function tells us to map v2 = 12 onto a vertex that dominates it in G2. We can see that vertex 3 dominates vertex 12 in G2. So, in our copwin spanning tree, there will be an edge between 12 and 3 (below).
Jeliazkova, Diana. 2006. Aspects of the cops and robber game played with incomplete information. Acadia University.
Now that we have defined a copwin spanning tree, S, let's look at schemes for placing alarms in a copwin graph to guarantee the capture of the robber.
Consider a copwin graph G with a given copwin ordering (x1, x2,. . . xn).
More Definitions!
More Definitions!
A vertex x of G is controlled if x remains free, while all neighbors of x are alarmed.
A path P of G is a freepath if all vertices of P are free.
A freepath P’ of G is isolated if all vertices of P’ are at distance at least three from any unalarmed vertex not in P’.
A collapsible freepath P’’ with vertices xi1 , xi2 , . . . , xim is almost isolated if P’’ is isolated in G − L(xi2 ), where L(xi2) is the set of leaves adjacent to xi2.
Assuming P’’ is an induced subgraph of G, the subgraph induced by V (P’’) ∪ L(xi2 ) is referred to as a free area.
Placing the Minimum Number of Alarms on a Copwin Graph
For a fixed copwin ordering (x1, x2, . . . , xn) of G, define ℵ(Sxn) as the minimum number of vertices with alarms, such that:
- Free vertices are either controlled or form collapsible freepaths (or free areas)
- Freepaths are induced subgraphs of G
- Freepaths are either isolated or almost isolated, and
- If an alarmed vertex xi has more than one unalarmed neighbor, then one of the following occcurs:
(a) xi is adjacent to a finite number of unalarmed leaves,
(b) xi lies on a collapsible path with exactly two controlled vertices,
(c) The unalarmed neighbors of xi lie on the same freepath P = xi1 , xi2 , . . . , xim, and i > im
(d) xi has exactly two unalarmed neighbors that lie on the same freepath P.
Define ℵG = minSv {ℵ(Sv)|Sv is a copwin spanning tree of G}.
Theorem:
This is a bit confusing because you have to look at both the original graph, G, and the copwin spanning tree, S, when placing the alarms. Overall, you want to configure the alarms such that the cop searches free areas and free paths until an alarm is triggered. Then the cop knows which free area the robber is leaving and which free area he is entering.
Conclusion
Like other variants of cops and robbers, Cop, Robber, and Alarms seems to be suited more towards playing on a computer. Cop, Robber, and Alarms can also be played with the alarms on the edges instead of on the vertices. Even further, this variant of Cops and Robbers can be played and analyzed with more than one cop. This idea of a game played with one cop and partial information about the location of the robber has many variations with different amounts and timings of the partial information. For example, in a witness version of the Cops and Robber game, cops have partial information provided via witnesses who report “sightings” of the robber. This is similar to the alarms version but sightings occur at regular intervals. Thus, the cop's strategy is different because she can just sit and wait for the witness to tell her the location of the robber. Overall, with the help of many many definitions of relationships between vertices, we can place the minimum number of alarms on a copwin graph to guarantee capture of the robber.
Works Cited
Clarke, N. E. (2009). A witness version of the Cops and Robber game. Discrete Mathematics, 3292-3298.
Connon, N. E. (2006). Cops, Robber, and Alarms. Ars Combinatoria -Waterloo then Winnipeg.
Jeliazkova, Diana. 2006. Aspects of the cops and robber game played with incomplete information. Acadia University.


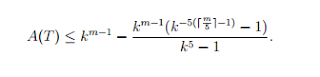


You did a good job explaining all the definitions and how to apply them!
ReplyDeleteFor the example you provided, would another combination of alarms be on r,h,e and l?
I was thinking the same thing because it is the mirror image of what is given. Is that the only option? How about b,e,i, and l?
DeleteI think that would be valid as well. It would just be a different scheme than the one she has (b/c it wouldn't satisfy her third condition).
DeleteYou're right Haley, h, e, and l would be another scheme satisfying those conditions. r isn't necessarily included but we can talk about that in class tomorrow.
DeleteNevin, b, e, i, and l would not be an alarm scheme satisfying the requirements because then a and h would not have exactly one unalarmed child.
DeleteGot it. Thanks.
DeleteGreat job Molli! Can you give an example of a collapsible free path in the copwin spanning tree in your example?
ReplyDeleteThanks Zach! A collapsible path in G would be 1, 5, 10. 1 is the root of the copwin spanning tree, S, so it must be an endpoint of the path in order for the path to be collapsible. Additionally, 1, 5, 10 is a collapsible path in G because it is also a path the the copwin spanning tree, S. It would be a collapsible free path if there were no alarms on it. We can talk more about the placement of alarms on a copwin graph in class.
DeleteJust a quick question about Cops, Robber, and Witness. I know you arent presenting on it, but do you know if the game involves 3 players? or is it similar to Cops, Robbers, and Alarms in the sense that the robbers position will be revealed every so often?
ReplyDeleteIt is similar to Cops, Robbers, and Alarms because the Robber's position is revealed every so often. So the "witness" isn't a player but actually just sort of a device, like the alarm is a device.
DeleteThis comment has been removed by the author.
ReplyDelete