Cops and Robbers: Capture Time

Before I begin discussing the Capture Time of a game of Cops and Robbers, there a few important concepts of Natasha’s talk that should be kept in mind:

1. The neighborhood of a vertex, call it v, is a set containing all the vertices v is adjacent to. We will denote this N(v).
2. A vertex v dominates a vertex u if N(u) is a subset of N(v).
3. A corner is a vertex in a graph that a robber can lose from, or more mathematically stated, u is a corner if there is some vertex v in the graph such that v dominates u.
4. A graph is dismantlable if it has a sequence of corners which when removed result in the trivial graph (a single vertex).
5. A graph is cop-win if and only if it’s dismantlable.

Now that we have all this in mind, there is some new vocab to learn.

1. In a game of Cops and Robbers, the length of the game is how many rounds it takes to capture the robber.
2. When playing the game, the play is considered optimal if the cops capture the robber in the least amount of time, assuming the robber is trying to maximize the length of the game.
3. The length of the optimal game is what we call the capture time of G, denoted capt(G).

What this means in English is that if we have a game of Cops and Robbers, where the robber is avoiding capture for a long as possible, then the capture time of G is the minimum number of turns it takes the cops to capture him.

If you want some practice with this idea, feel free to try and work out the capture time for the graphs below, and leave your answer in the comments section. We’ll also work through these two examples in class, so don’t worry too much if this is still confusing. 

G1

G2

While it is relatively easy to determine the capture time of individual graphs, there are an infinite number of graphs, and it is impossible to compute the capture time of them all. For this reason, we need to characterize graphs to help us determine their capture time. The following proofs will help us to determine the upper bound on the capture time of certain types of graphs.

How can we determine Capture Time?

Theorem 1:

If G is a cop-win graph, then capt(G) ≤ n-1, where n is the number of vertices in G.

This proof is dense, but if you would like to read it, you can find it under the heading Theorem 1.2.3 here.

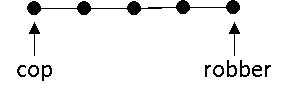
It is a rather logical argument though. Let’s think about the longest game it is possible to play on a cop-win graph. As an example, use the basic tree graph, with n vertices. If a cop starts at one end, and robber starts at the other, then the cop will always move closer to the robber while the robber will stay put. The longest time a game played this way will take is n-1 turns. This means n-1 is our upper bound for the capture time, so capt(G) ≤ n-1.

In an example with five vertices, the cop starts on the left side, while the robber starts on the right:

On each turn, the cop moves one closer to the robber.

So, the longest time this game can take is four turns, or the number of vertices minus one. We know the capture time must be smaller than or equal to this, since the capture time is the minimum number of turns it takes to win. And since there is no way to play this graph with five moves, our upper bound of n-1 (4 in this case) makes sense.

Improvement on the Upper Bound

We can do better than that though. It turns out the following is true:

If G is a cop-win graph of order n ≥ 5, then capt(G) ≤ n-3.

Proof by Induction:

Base Case: n=5

This holds true for n=5, because you can check all cop-win graphs of order 5 and see that it does.

Inductive Step:

Suppose the theorem holds true for graphs of order n≥5, and assume G has n+1 vertices.

Then G has a corner, u, and since by deleting that corner we get back to a graph with n vertices, the graph G is cop-win.

By the induction hypothesis, the cop can capture the robber in the graph G – u in at most n-3 rounds. So in G, if the robber is not on u, then the cop plays her winning strategy, and can win in n-3 rounds. If the robber is on u, then the cop will only be one vertex away and can win in (n+1)-3 moves.

For more information on this proof, see The Games of Cops and Robber on Graphs by Bonato and Nowakowski, page 36.

Further Improvement on the Upper Bound

It turns out we can do even better though. Some graphs have two separate corners, which when removed make another graph with two separate corners. If those two vertices can be removed, to make another graph with two separate corners, and so on until the graph has less than seven vertices, then the graph is called 2-dismantlable.

It turns out, if G is 2-dismantlable of order n, then capt(G) ≤ n/2.

This is another proof by induction, which I will leave as an exercise for the reader if they are so inclined. If not, you can find it in The Games of Cops and Robber on Graphs by Bonato and Nowakowski, page 216.

We'll do an example of this type of graph in class, because it's rather involved, but if you have any questions before than please leave them in the comments section!

More Improvement on the Upper Bound

The following characterization of graphs relates to the final example Natasha gave us on Thursday.

This graph belongs to a special group of graphs that we know the exact capture time of.

If a graph G is planar, cop-win with a unique corner and has n ≥ 7 vertices, then capt(G) = n-4.

So, what’s the capture time of the graph above? Three. In order for the cop to catch the robber, she needs at least three turns, assuming the robber plays optimally.

If you are interested in the proof for this theorem, see The Games of Cops and Robber on Graphs by Bonato and Nowakowski, page 217.

Capture Time with More Than One Cop

So far everything we’ve done has dealt with graphs that have a cop number of 1. What about graphs that need more cops? Research is still ongoing in this area, but the basic ideas of capture time apply the same way to graphs with more than one cop.

One example would be the 4-cycle graph from class, which needed two cops to make it cop-win.

What is the capture time of this graph? Leave your answer in the comments below.

Conclusion

The capture time of graph is important because it tells us how quickly the cops can catch the robber, even if the robber is trying to evade capture for as long as possible. There is no definite answer as to what the capture time of any given graph is, especially when you complicate it by adding more cops. Research is ongoing, and at the moment the best we can do to estimate the capture time of a graph is to use the bounds proven above. 

Citations:

Bonato, Anthony, and Richard J. Nowakowski. The Game of Cops and Robbers on Graphs. Providence, RI: American Mathematical Society, 2011. Print.

Bonato, A., P. Golovach, G. Hahn, and J. Kratochvi­l. "The Capture Time of a Graph."Discrete Mathematics 309.18 (2009): 5588-595. Web.

Clarke, Nancy E. Constrained Cops and Robbers. Diss. Dalhousie U, 2002. Ottawa: National Library of Canada, 2002. Print.